(本小题满分12分)在直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系.已知曲线
轴的正半轴为极轴,建立极坐标系.已知曲线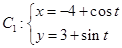 (
(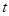 为参数),
为参数), (
( 为参数).
为参数).
(Ⅰ)化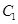 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若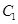 上的点
上的点 对应的参数为
对应的参数为 ,
,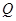 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线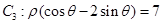 距离的最小值.
距离的最小值.
(本小题满分14分)
已知函数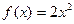 ,
,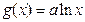 (
(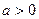 ).
).
(1)当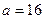 时,试求函数
时,试求函数 在
在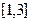 上的值域;
上的值域;
(2)若直线 交
交 的图象
的图象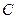 于
于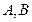 两点,与
两点,与 平行的另一直线
平行的另一直线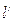 与图象
与图象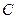 切于点
切于点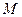 .
.
求证: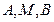 三点的横坐标成等差数
三点的横坐标成等差数 列;
列;
(本小题满分14分)
已知椭圆方程为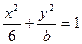 (
(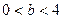 ),抛物线方程为
),抛物线方程为 .过抛物线的焦点作
.过抛物线的焦点作 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为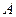 ,抛物线在点
,抛物线在点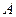 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点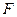 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设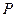 为椭圆上的动点,由
为椭圆上的动点,由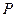 向
向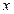 轴作垂线
轴作垂线 ,垂足为
,垂足为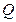 ,且直线
,且直线 上一点
上一点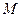 满足
满足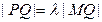 ,求点
,求点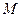 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
(本小题满分14分)
已知等差数列 的公差
的公差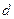 大于0,且
大于0,且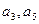 是方程
是方程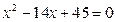 的两根,数列
的两根,数列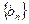 的前
的前 项的和为
项的和为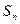 ,且
,且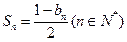 .
.
(1)求数列 ,
,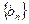 的通项公式;
的通项公式;
(2)记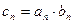 ,求证:
,求证: ;
;
(3)求数列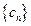 的前
的前 项和.
项和.
(本小题满分13分)
已知等差数列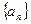 的公差为
的公差为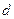 ,前
,前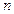 项和为
项和为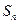 ,且满足
,且满足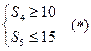 ,
,
(1)试用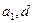 表示不等式组
表示不等式组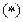 ,并在给定的坐标系中用阴影画出不等式组表示的平面区域;
,并在给定的坐标系中用阴影画出不等式组表示的平面区域;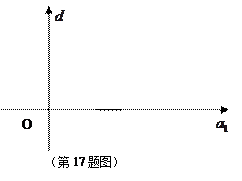 (2)求
(2)求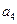 的最大值,并指出此时数列
的最大值,并指出此时数列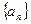 的公差
的公差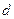 的值.
的值.
(本小题满分13分)
已知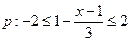 ,
, ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数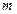 的取值范围.
的取值范围.