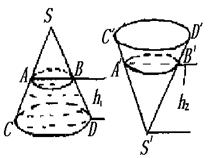
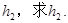(本小题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班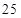 名女同学,
名女同学,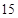 名男同学中随机抽取一个容量为
名男同学中随机抽取一个容量为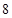 的样本进行分析.随机抽出
的样本进行分析.随机抽出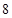 位,他们的数学分数从小到大排序是:
位,他们的数学分数从小到大排序是: 、
、 、
、 、
、 、
、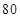 、
、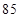 、
、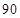 、
、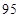 ,物理分数从小到大排序是:
,物理分数从小到大排序是: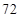 、
、 、
、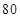 、
、 、
、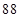 、
、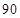 、
、 、
、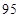 .
.
(Ⅰ)如果按性别比例分层抽样,男女同学分别抽取多少人?
(Ⅱ)若这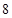 位同学的数学、物理分数对应如下表:
位同学的数学、物理分数对应如下表:
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
| 物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量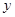 与
与 的相关系数或散点图说明物理成绩
的相关系数或散点图说明物理成绩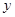 与数学成绩
与数学成绩 之间是否具有线性相关性?如果具有线性相关性,求
之间是否具有线性相关性?如果具有线性相关性,求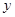 与
与 的线性回归方程(系数精确到
的线性回归方程(系数精确到 );如果不具有线性相关性,请说明理由.
);如果不具有线性相关性,请说明理由.
参考公式:相关系数 ;回归直线的方程是:
;回归直线的方程是: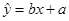 .
.
其中对应的回归估计值:
参考数据: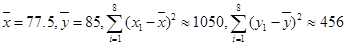 ,
, .
.
(本小题满分10分)已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设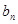 =
=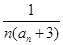 (n∈N*),
(n∈N*),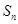 =b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有
=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有 总成立?若存在,求出t;若不存在,请说明理由
总成立?若存在,求出t;若不存在,请说明理由
(本小题满分10分)已知A、B、C为△ABC的三内角,且其对边分别为a、b、c.若 ,
, 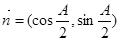 ,且
,且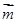 ·
· =
= .
.
(1) 求角A的大小; ⑵ 若a=2 ,三角形面积S=
,三角形面积S= ,求b+c的值.
,求b+c的值.
(本小题14分)已知四棱锥P-ABCD,底面ABCD是 、边长为
、边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.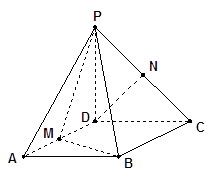
(1)证明:DN//平面PMB;
(2)证明:平面PMB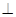 平面PAD;
平面PAD;
(3)求点A到平面PMB的距离.
(本小题满分10分)如图,在三棱柱 —
— 中,点D是BC的中点,欲过点
中,点D是BC的中点,欲过点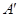 作一截面与平面
作一截面与平面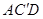 平行,问应当怎样画线,并说明理由。
平行,问应当怎样画线,并说明理由。
(本小题10分)如图,圆锥形封闭容器,高为h,圆锥内水面高为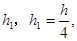 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为