(本题14分)如图①,直线 :
: 分别与
分别与 轴、
轴、 轴交于A、B两点,与直线
轴交于A、B两点,与直线 :
: 交于点
交于点 .
.
(1)求A、B两点坐标及 、
、 的值;
的值;
(2)如图②,在线段BC上有一点E,过点E作 轴的平行线交直线
轴的平行线交直线 于点F,过E、F分别作EH⊥
于点F,过E、F分别作EH⊥ 轴,FG⊥
轴,FG⊥ 轴,垂足分别为H、G,设点E的横坐标为
轴,垂足分别为H、G,设点E的横坐标为 ,当
,当 为何值时,矩形EFGH的面积为
为何值时,矩形EFGH的面积为 ;
;
(3)若点P为 轴上一点,则在平面直角坐标系中是否存在一点Q,使得P、Q、A、B四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
轴上一点,则在平面直角坐标系中是否存在一点Q,使得P、Q、A、B四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
玉树地震发生后,根据救灾指挥中心的信息,甲、乙两个重灾区急需一种大型挖掘机,甲地需要27台,乙地需要25台;A、B两省获知情况后慷慨相助,分别捐赠该型号挖掘机28台和24台,并将其全部调运往灾区,如果从A省调运一台挖掘机到甲地耗资0.4万元,到乙地耗资0.3万元;从B省调运一台挖掘机到甲地耗资0.5万元,到乙地耗资0.2万元;设从A调往甲地x台挖掘机,A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元:
(1)请完成表格的填空:
(2)求出y与x之间的函数关系式,并直接写出自变量x的取值范围
(3)画出这个函数的图象,结合图象说明若要使总耗资不超过16.2万元,有哪几种调运方案?哪种调运方案的总耗资最少?
(1)点(1,3)沿X轴的正方向平移4个单位得到的点的坐标是_________
(2)直线y=3x沿x轴的正方向平移4个单位得到的直线解析式为____________
(3)若直线l与(2)中所得的直线关于直线x=2对称,试求直线l的解析式.
如图1:直线y= kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点M的直线BD交x轴于点B,交y轴于点D.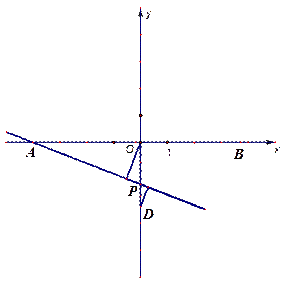
(1)求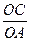 的值(用含有k的式子表示.);
的值(用含有k的式子表示.);
(2)若S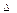 BOM =3S
BOM =3S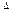 DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=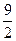 的根,求直线BD的解析式.
的根,求直线BD的解析式.
(3)如图2,在(2)的条件下,P为线段OD之间的动点(点P不与点O和点D重合),OE
上AP于E,,DF上AP于F,下列两个结论:①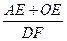 值不变;②
值不变;②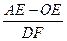 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.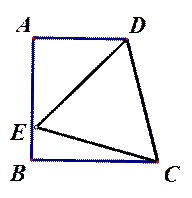
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求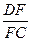 的值.
的值.
已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB.
(1)若A、B的位置如图l所示,试化简:  -
- +
+ +
+

(2)如图2,若 +
+ =8.9,MN=3,求图中以A、N、O、M、B这5个点为端点的所
=8.9,MN=3,求图中以A、N、O、M、B这5个点为端点的所
有线段长度的和;
(3)如图3,M为AB中点,N为OA中点,且MN=2AB-15,a=-3,若点P为数轴上一点,且PA= AB,试求点P所对应的数为多少?
AB,试求点P所对应的数为多少?