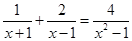（本题共12分）定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．
（1）已知：如图1，四边形
是“等对角四边形”，
，
，
．求
，
的度数．
（2）在探究“等对角四边形”性质时：
① 小红画了一个“等对角四边形”（如图2），其中
，
，此时她发现
成立．请你证明此结论．
② 由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．
（3）已知：在“等对角四边形”中，
，
，
，
．求对角线
的长．
列方程解应用题
某一工程进行招标时，接到了甲、乙两个工程队的投标书，施工1天需付甲工程队工程款1.5万元，付乙工程队工程款1.1万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案： 方案（1）：甲工程队单独完成这项工程，刚好如期完成；方案（2）：乙工程队单独完成这项工程，要比规定日期多5天；方案（3）：若甲、乙两队合作4天，余下的工程由乙工程队单独做，也正好如期完成；在不耽误工期的情况下，你觉得哪种方案最省钱？请说明理由。
如图，△ABC中，∠ACB=90度，AC=7，BC=24，CD⊥AB于D。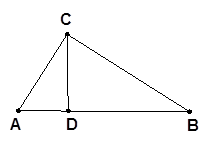
（1）求AB的长；
（2）求CD的长。
如图，△ACB和△ECD都是等腰直角三角形，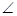
ACB=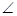ECD=90°．D为AB边上一点．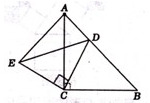 
求证：(1)△ACE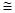
△BCD；
(2)AD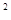
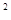+DB=DE．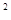
先化简代数式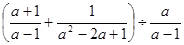
，然后选取一个使原式有意义的
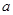的值代入求值.
解方程：