如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,4),B(﹣3,5),C(﹣4,1).
(1)把△ABC向右平移2个单位得△A1B1C1,请画出△A1B1C1,并写出点A1的坐标;
(2)把△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.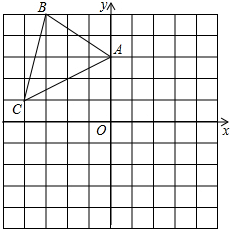
如图,已知∠1=36°,当∠2等于多少度时,AB∥CD?请说明理由.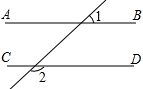
如图,∠1=∠2,AC平分∠DAB,求证:DC∥AB.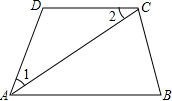
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.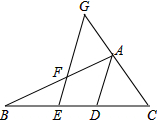
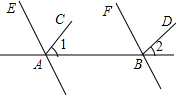
看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:∵∠1=35°,∠2=35°(已知),
∴∠1=∠2
∴_______∥_______(同位角相等,两条直线平行)
又∵AC⊥AE(已知),
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=_______°(等式的性质)
同理可得,∠FBD+∠2=_______°
∴_______∥_______(同位角相等,两条直线平行)