(本题8分)计算:
(1)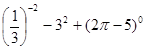
(2)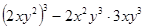
在等腰△ABC中,三边分别为 其中
其中 =5,若关于
=5,若关于 的方程
的方程 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
已知关于x的方程 .
.
(1)若此方程有两个不相等的实数根,求a的范围;
(2)在(1)的条件下,当a取满足条件的最小整数,求此时方程的解.
按要求解下列一元二次方程:
(1) (配方法);
(配方法);
(2) (公式法).
(公式法).
解下列一元二次方程:
(1)
(2)
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.