在一个不透明的盒子里,装有三个分别写有数字6, 2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
(本题8分)设 ,
, ,且
,且 ,求
,求 的值.
的值.
(本题6分)如图,平面内有A、B、C、D 四点,按下列语句画图:
(1)画射线AB,直线BC,线段AC;
(2)延长CA;
(3)连接AD与BC相交于点E.
将一副三角板放在同一平面,使直角顶点重合于点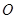 .
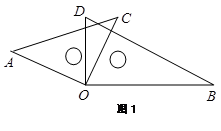
.
(1)如图1,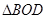 保持不动,把
保持不动,把 绕着点
绕着点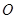 旋转,使得
旋转,使得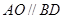 ,求
,求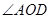 的度数.
的度数.
(2)当 与
与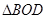 重叠时,直接写出
重叠时,直接写出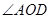 与
与 的大小关系。
的大小关系。
(3)如图1,若 ,求
,求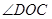 的度数。
的度数。
你发现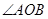 与
与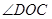 存在怎样的数量关系?用式子直接表示出来。
存在怎样的数量关系?用式子直接表示出来。
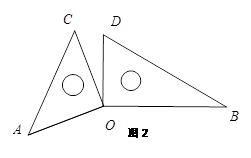
(4)如图2,当 与
与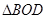 不重叠时,(3)中
不重叠时,(3)中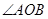 与
与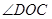 关系式是否成立,请简要说明理由.
关系式是否成立,请简要说明理由.
 |
某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整(扇形统计图填上“一般”的百分率,条形统计图上画出“优秀”的条形图);
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
某个体商贩在一次买卖中同时买进两件上衣,每件都以a元出售,若按成本计算,一件盈利25%,另一件亏本25%,那么该商贩在这次买卖过程中是赚了还是赔本了?赚或赔多少?