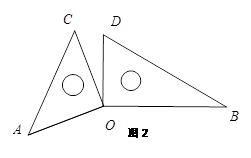
将一副三角板放在同一平面,使直角顶点重合于点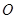 .
.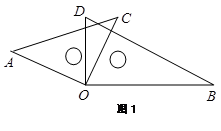
(1)如图1, 保持不动,把
保持不动,把 绕着点
绕着点 旋转,使得
旋转,使得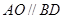 ,求
,求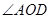 的度数.
的度数.
(2)当 与
与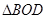 重叠时,直接写出
重叠时,直接写出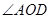 与
与 的大小关系。
的大小关系。
(3)如图1,若 ,求
,求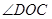 的度数。
的度数。
你发现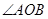 与
与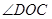 存在怎样的数量关系?用式子直接表示出来。
存在怎样的数量关系?用式子直接表示出来。
(4)如图2,当 与
与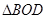 不重叠时,(3)中
不重叠时,(3)中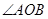 与
与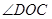 关系式是否成立,请简要说明理由.
关系式是否成立,请简要说明理由.
 |
(年四川巴中12分)如图,在平面直角坐标系xOy中,抛物线 与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.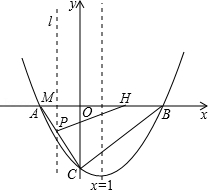
(1)求抛物线的解析式;
(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原
点时,点H立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
(年山东烟台10分)在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;
(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.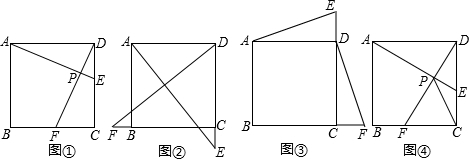
(年江苏无锡10分)如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.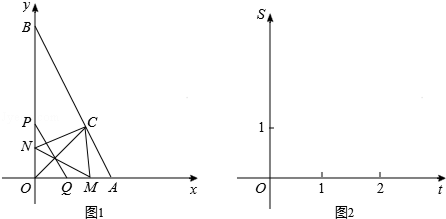
(年湖南娄底10分)如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: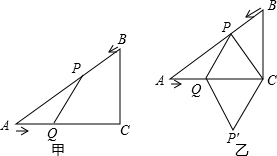
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?
(2014年湖北襄阳12分)如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?