(年四川巴中12分)如图,在平面直角坐标系xOy中,抛物线 与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.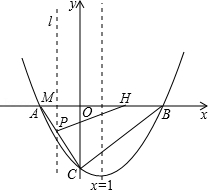
(1)求抛物线的解析式;
(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原
点时,点H立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A1、B2,求△OA1B2的面积。
已知,如图在直角梯形ABCD中,AD∥BC,∠A=900,BC=CD=10,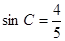 ,
,
(1)求梯形ABCD的面积;
(2)点E、F分别是BC、CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1个单位的速度同时出发,连接EF,求△EFC面积的最大值,并说明此时E、F的位置。
小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,游戏规则如下:
(1)请用树状图或列表法表示一个回合所有可能出现的结果。
(2)求一个合能确定两人先下棋的概率。
如图,在△ABC中,∠A=300, ,BC=
,BC= ,求AB的长。
,求AB的长。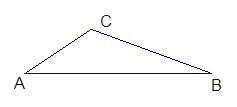
如图,抛物线与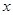 轴交于
轴交于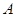 (
(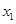 ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且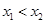 ,与
,与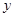 轴交于点
轴交于点 ,其中
,其中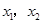 是方程
是方程 的两个根。
的两个根。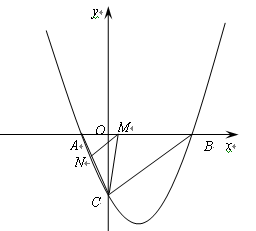
(1)求抛物线的解析式;
(2)点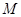 是线段
是线段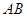 上的一个动点,过点
上的一个动点,过点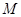 作
作 ∥
∥ ,交
,交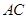 于点
于点 ,连接
,连接 ,当
,当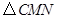 的面积最大时,求点
的面积最大时,求点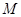 的坐标;
的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点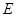 为抛物线上一动点,在
为抛物线上一动点,在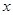 轴上是否存在点
轴上是否存在点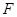 ,使以
,使以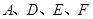 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。