如图,平面直角坐标系中O为坐标原点,直线y=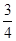 x+6与x轴、y轴分别交于A、B两点,C为OA中点;
x+6与x轴、y轴分别交于A、B两点,C为OA中点;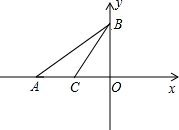
(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒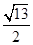 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?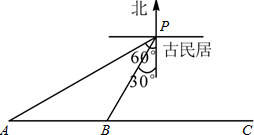
下表是初三某班女生的体重检查结果:
| 体重(kg) |
34 |
35 |
38 |
40 |
42 |
45 |
50 |
| 人数 |
1 |
2 |
5 |
5 |
4 |
2 |
1 |
根据表中信息,回答下列问题:
(1)该班女生体重的中位数是;
(2)该班女生的平均体重是kg;
(3)根据上表中的数据补全条形统计图.
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使 .
.
解不等式组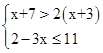 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.