如图，在平面直角坐标系中，抛物线
，经过A（0，﹣4），B（
，0），C（
，0）三点，且
．
（1）求b，c的值；
（2）在抛物线上求一点D，使得四边形BDCE是以BC为对角线的菱形；
（3）在抛物线上是否存在一点P，使得四边形BPOH是以OB为对角线的菱形？若存在，求出点P的坐标，并判断这个菱形是否为正方形？若不存在，请说明理由．
如图，把长方形纸片ABCD沿EF折叠，使点D与点B重合，点C落在点C′的位置上．
⑴若∠1=50°，求∠2、∠3的度数；
⑵若AB=7，DE=8，求CF的长度．
如图，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．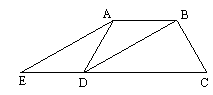
⑴求证：梯形ABCD是等腰梯形．
⑵若∠BDC＝30°，AD＝5，求CD的长．
已知如下图，正方形ABCD中，E是CD边上的一点，F为BC延长线上点，CE="CF."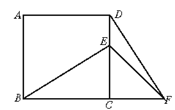 
(1)求证：△BEC≌△DFC；
(2)若∠BEC=60°，求∠EFD的度数
射击队对甲、乙两名运动员进行了六次测试，测试成绩如下表（单位：环）：
分别计算甲、乙六次测试成绩的方差；
如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，
求证：CE=CF。