如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.如图1,矩形ABCD中,AB=3,BC=1,请在边AB上作出C,D两点的所有勾股点(要求:尺规作图,保留作图痕迹,不要求写作法).
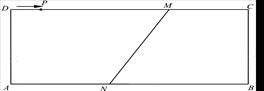
如图2,矩形ABCD中,AB=12cm,BC=4 cm,DM=8 cm,AN=5 cm.动点P从D点出发沿着DC方向以1 cm/s的速度向右移动,过点P的直线l平行于BC,当点P运动到点M时停止运动.设运动时间为t(s) ,点H为M,N两点的勾股点,且点H在直线l上.
①当t=4、 t=5时,直接写出点H的个数.②探究满足条件的点H的个数(直接写出点H的个数及相应t的取值范围,不必证明).
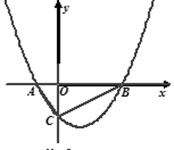
如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.求a的值;
求A,B的坐标;
以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.
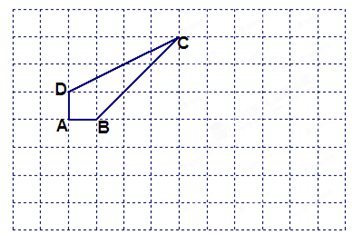
已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.在所给网格中按下列要求画图:
在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);
将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;写出C”、D”的坐标;
请判断四边形A”B”C”D”与四边形ABCD成何种对称?若成中心对称,请写出对称中心; 若成轴对称,请写出对称轴.
如图,已知抛物线y=ax2+bx+c经过 A(0,4),B(4,0),C(–1,0)三点.过点A作垂直于y轴的直线l. 在抛物线上有一动点P,过点P作直线PQ平行于y轴交直线l于点Q .连结AP.求抛物线y=ax2+bx+c的解析式;
是否存在点P,使得以A、P、Q三点构成的三角形与△AOC相似.如果存在,请求出点P的坐标,若不存在,请说明理由;
当点P位于抛物线y=ax2+bx+c的对称轴的右侧.若将△APQ沿AP对折,点Q的对应点为点M.求当点M落在坐标轴上时直线AP的解析式.

如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.求证:MN是半圆的切线;
求证:FD=FG;
若△DFG的面积为4.5,且DG=3,GC=4,试求△BCG的面积.
