某商场统计了今年1～5月A，B两种品牌冰箱的销售情况，并将获得的数据绘制成折线统计图．
（1）分别求该商场这段时间内A，B两种品牌冰箱月销售量的中位数和方差；
（2）根据计算结果，比较该商场1～5月这两种品牌冰箱月销售量的稳定性．
已知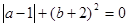
，求（a＋b）
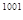的值.
有七名学生称了体重，以48.0千克为标准，把超过标准体重的部分记为正数，不足标准体重的部分记为负数，将其体重记录如下表：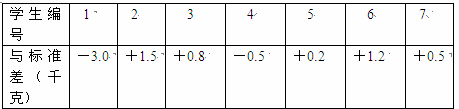
（1）最接近标准体重的学生体重是多少？
（2）求七名学生的平均体重；
（3）若按体重的轻重排列时，则恰好居中的是哪号学生？
画出数轴，用数轴上的点表示下列各数，并用“＞”将它们连接起来：3，－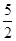
，1.5，－0.5.
一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面和从左面看到的这个几何体的形状图。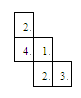
化简求值：
（1）6a＋7a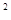
－5a－6a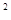，其中a=－3；
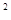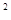（2）2（ab＋ab）－3（a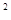b－1）－2ab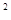－2，其中a=－2，b=2.