有七名学生称了体重,以48.0千克为标准,把超过标准体重的部分记为正数,不足标准体重的部分记为负数,将其体重记录如下表: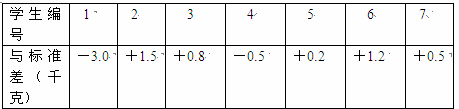
(1)最接近标准体重的学生体重是多少?
(2)求七名学生的平均体重;
(3)若按体重的轻重排列时,则恰好居中的是哪号学生?
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
求证:(1)△ABC≌△DEF;(2)GF=GC。
(要求:写出重要证明依据)
(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。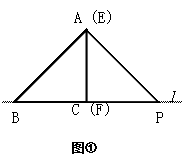
阅读材料,解答下列问题.
例:当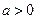 时,如
时,如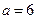 则
则 ,故此时
,故此时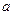 的绝对值是它本身
的绝对值是它本身
当 时,
时, ,故此时
,故此时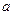 的绝对值是零
的绝对值是零
当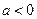 时,如
时,如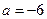 则
则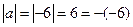 ,故此时
,故此时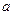 的绝对值是它的相反数
的绝对值是它的相反数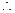 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即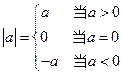
问:(1)这种分析方法涌透了数学思想.
(2)请仿照例中的分类讨论的方法,分析二次根式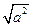 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想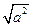 与
与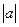 的大小关系.
的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题: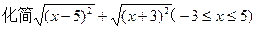
(1)计算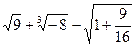
(2)解方程: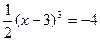
(3)计算:
国际比赛的足球场地是在100米到110米之间,宽是在64米到75米之间,现有一个长方形的足球场,其长是宽的1.5倍,面积是7560平方米,那么这个足球场能用作国际比赛吗?(参考数据: )
)