某蔬菜培育中心决定向某灾区配送无辐射蔬菜和水果共3200箱,其中水果比蔬菜多800箱.
(1)求水果和蔬菜各有多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批水果和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装水果400箱和蔬菜100箱,每辆乙种货车最多可装水果和蔬菜各200箱,则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费4000元,乙种货车每辆需付运费
3600元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.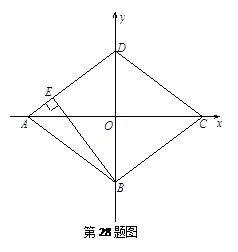
填空:菱形ABCD的边长是▲ 、面积是▲ 、
高BE的长是▲ ;探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得▲APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形,并求出k的值
如图(1),点M,N分别在等边△ABC的BC,AC边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60°
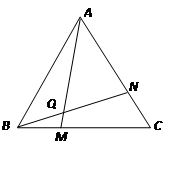
判断下列命题的真假性:
①若将题(1)中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题(1)中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?(如图2)
③若将题(1)中的条件“点M,N分别在正△ABC的BC,AC边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?(如图3)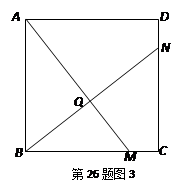
在下列横线上填写“是”或“否”:①▲;②▲;③▲.并对②,③的判断,选择其中的一个给出证明.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
求证:BC与⊙O相切
若OC⊥BD,垂足为E,BD=6,CE=4,求AD的长.
已知抛物线 经过点
经过点 和点P(t,0),且t≠0
和点P(t,0),且t≠0若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值;
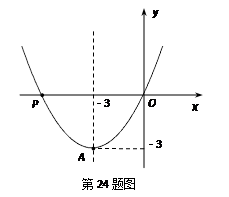
若
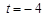 ,求a、b的值,并指出此时抛物线的开口方向
,求a、b的值,并指出此时抛物线的开口方向直接写出使该抛物线开口向下的t的一个值
周六下午,小刚到小强家玩.休息之余,两人进入校园网,研究起了本校各班的课程表……
现已知初一(1)班周四下午共安排数学、生物、体育这三节课请你通过画树状图列出初一(1)班周四下午的课程表的所有可能性;
小刚与小强通过研究发现,学校在安排课务时遵循了这样的一个原则——在每天的课表中,语文、数学、英语这三门学科一定是安排在体育课之前的.请问你列出的初一(1)班周四下午的课程表中符合学校课务安排原则的概率是多少?