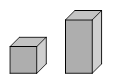
如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
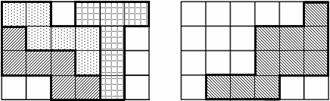
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).
|
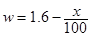 ,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线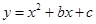 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.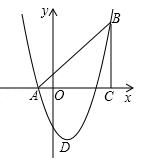
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;
②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
情境观察
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 ,∠CAC′= °.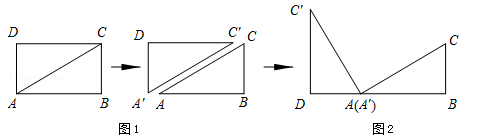
问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸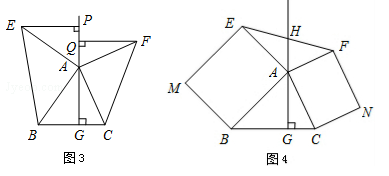
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.
某批发商以40元/千克的成本价购入了某产品700千克,据市场预测,该产品的销售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x,但保存这批产品平均每天将损耗15千克,且最多保存15天.另外,批发商每天保存该批产品的费用为50元.
(1)若批发商在保存该产品5天时一次性卖出,则可获利 元.
(2)如果批发商希望通过这批产品卖出获利10000元,则批发商应在保存该产品多少天时一次性卖出?
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.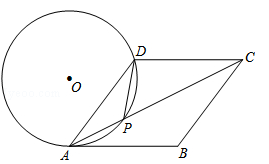
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC=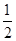 ,求⊙O的半径.
,求⊙O的半径.
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: (即AB:BC=1:
(即AB:BC=1: ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).