【试题背景】已知:l ∥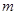 ∥
∥ ∥k,平行线l与
∥k,平行线l与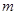 、
、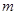 与
与 、
、 与k之间的距离分别为
与k之间的距离分别为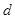 1、
1、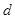 2、
2、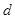 3,且
3,且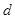 1 =
1 =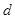 3 = 1,
3 = 1,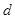 2 =" 2" .我们把四个顶点分别在l、
2 =" 2" .我们把四个顶点分别在l、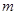 、
、 、k这四条平行线上的四边形称为“格线四边形”.
、k这四条平行线上的四边形称为“格线四边形”.
【探究1】(1)如图1,正方形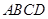 为“格线四边形”,
为“格线四边形”, 于点
于点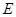 ,
,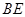 的反向延长线交直线k于点
的反向延长线交直线k于点 . 求正方形
. 求正方形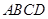 的边长.
的边长.
【探究2】(2)矩形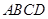 为“格线四边形”,其长 :宽 =" 2" :1 ,则矩形
为“格线四边形”,其长 :宽 =" 2" :1 ,则矩形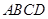 的宽为 .(直接写出结果即可)
的宽为 .(直接写出结果即可)
【探究3】(3)如图2,菱形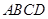 为“格线四边形”且∠
为“格线四边形”且∠ =60°,△
=60°,△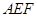 是等边三角形,
是等边三角形, 于点
于点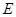 , ∠
, ∠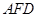 =90°,直线
=90°,直线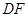 分别交直线l、k于点
分别交直线l、k于点 、
、 . 求证:
. 求证: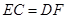 .
.
【拓 展】(4)如图3,l ∥k,等边三角形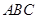 的顶点
的顶点 、
、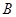 分别落在直线l、k上,
分别落在直线l、k上,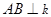 于点
于点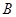 ,且
,且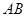 ="4" ,∠
="4" ,∠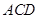 =90°,直线
=90°,直线 分别交直线l、k于点
分别交直线l、k于点 、
、 ,点
,点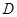 、
、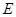 分别是线段
分别是线段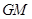 、
、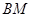 上的动点,且始终保持
上的动点,且始终保持 =
=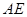 ,
, 于点
于点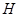 .
.
猜想: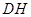 在什么范围内,
在什么范围内, ∥
∥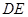 ?直接写出结论。
?直接写出结论。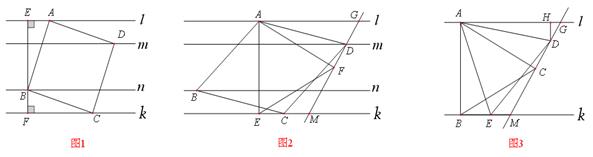
姚明作为我国最优秀的篮球运动员转会至美国NBA,一方面推动我国篮球事业的快速发展,同时也给他所加入的NBA俱乐部带来更大的商机,它将拥有来自世界人口最多的国家的广大球迷爱好者和姚明的崇拜者,使得凡是姚明所参加的每一场NBA球赛能获得更多的观众收视率。如果要对姚明最近一场球赛的收视率在国内进行调查,是否每个看电视的人都要被问到?仅对六十岁以上的老年同志的调查结果能否作为该场比赛的国内收视率?你认为应该怎样调查更合适些?
为了完成下列任务,你认为采用什么调查方式更合适?
(1)了解你们班同学周末时间是如何安排的.
(2)了解一批圆珠笔芯的使用寿命.
(3)了解我国八年级学生的视力情况.
2003年5月,一场抗击非典肺炎的 “战争”在全国各地进行着,为了获得每天感染非典患者,疑似病例患者的数据,需要对十二亿多人进行普查吗?你认为采取什么调查方式更适合?请结合实际情况谈谈你的想法。
查阅动物百科全书可以知道:喜鹊体长41~52cm,营巢于高大乔木的中上层,每次产卵5~8枚;丹顶鹤体长约140cm,营巢于周围环水的浅滩或深草丛中,每次产卵2枚;绿孔雀体长100~230cm,营巢于灌木丛.竹丛间的地面,每次产卵4~8枚;鸳鸯体长38~44cm,营巢于树洞中,每次产卵7~12枚,请用一张统计表简洁地表示上述信息,并谈谈你从这些信息中发现了什么?
为了考察一批树苗的高度,从中抽出10株,量得结果如下(单位:cm):11,12,11,13,12,14,11,13,11,14
(1)在这个问题中,总体,个体,样本各是什么?
(2)在这个样本中其众数,中位数,平均数各是什么?
(3)试估计这一批树苗的平均高度。