解方程:
(1)2x+7=52﹣3x;
(2)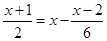 .
.
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2008年,A市在省财政补助的基础上再投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2008年到2010年,A市三年共投资“改水工程”多少万元?
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.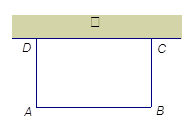
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
如图所示,作出△ABC关于点O成中心对称的图形△A1B1C1.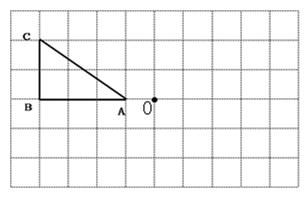
当 为何值时,关于x的一元二次方程
为何值时,关于x的一元二次方程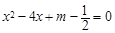 有两个相等的实数根?此时这两个实数根是多少?
有两个相等的实数根?此时这两个实数根是多少?
用适当的方法解下列一元二次方程: .
.