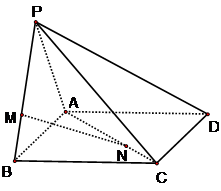
(本小题满分9分)如图,在四棱锥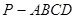 中,侧面
中,侧面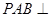 底面
底面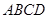 ,侧面
,侧面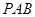 是边长为3的等边三角形,底面
是边长为3的等边三角形,底面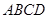 是正方形,
是正方形,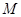 是侧棱
是侧棱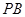 上的点,
上的点,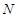 是底面对角线
是底面对角线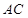 上的点,且
上的点,且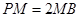 ,
,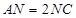 .
.
(Ⅰ)求证: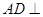
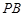 ;
;
(Ⅱ)求证: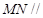 平面
平面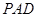 ;
;
(Ⅲ)求点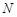 到平面
到平面 的距离.
的距离.
(本题满分13分)已知光线经过已知直线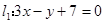 和
和 的交点
的交点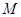 , 且射到
, 且射到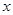 轴上一点
轴上一点 后被
后被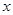 轴反射.
轴反射.
(1)求点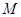 关于
关于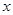 轴的对称点
轴的对称点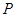 的坐标;
的坐标;
(2)求反射光线所在的直线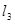 的方程.
的方程.
(3)
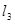
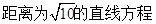
(本小题满分12分)已知函数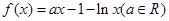 .
.
(Ⅰ)讨论函数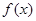 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数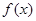 在
在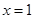 处取得极值,对
处取得极值,对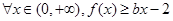 恒成立,求实数
恒成立,求实数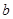 的取值范围.
的取值范围.
(本小题满分12分)已知: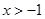 ,证明:
,证明: 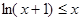
(本小题满分12分)设某物体一天中的温度 是时间
是时间 的函数:
的函数: ,其中温度的单位是
,其中温度的单位是 ,时间单位是小时,
,时间单位是小时, 表示12:00,
表示12:00, 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是 ,12:00的温度为
,12:00的温度为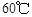 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度 关于时间
关于时间 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数 在区间
在区间 上的平均值为
上的平均值为 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
已知函数 的图象过点
的图象过点 ,且在点
,且在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数 的单调区间.
的单调区间.