在初中数学中,我们学习了“两点间的距离”、“点到直线的距离”、“平行线之间的距离”,距离的本质是“最短”,图形之间的距离总可以转化为两点之间的距离,如“垂线段最短”的性质,把点到直线的距离转化为点到点(垂足)的距离.
一般的,一个图形上的任意点A与另一个图形上的任意点B之间的距离的最小值叫做两个图形的距离.
(1)如图1,过A,B分别作垂线段AC、AD、BE、BF,则线段AB和直线l的距离为垂线段 的长度.
(2)如图2,Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB,AD=2,那么线段AD与线段BC的距离为 .
(3)如图3,若长为1cm的线段CD与已知线段AB的距离为1.5cm,请用适当的方法表示满足条件的所有线段CD.
注:若满足条件的线段是有限的,请画出;若满足条件的线段是无限的,请用阴影表示其所在区域.(保留画图痕迹)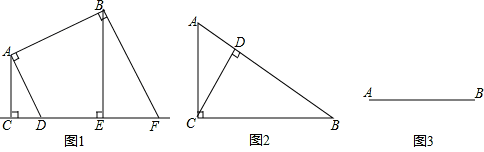
如图,已知线段a及∠O,只用直尺和圆规,求做△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)
如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上,按要求画一个三角形,使它的顶点在方格的顶点上。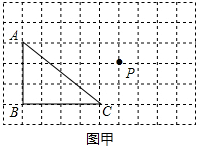
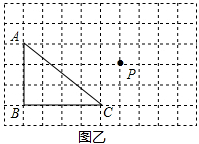
(1)将△ABC平移,使点P落在平移后的三角形内部,在图甲中画出示意图;
(2)以点C为旋转中心,将△ABC旋转,使点P落在旋转后的三角形内部,在图乙中画出示意图。
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E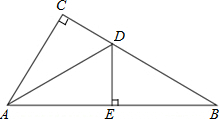
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
化简: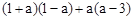
计算: ;
;