如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【原创】实数a,b,c在数轴上的位置如图所示,化简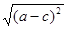 -|a+b|-|b+c|=
-|a+b|-|b+c|=
【改编】如图,有一个直角三角形ABC,∠ACB=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在射线AC和过点A且垂直于AC的射线AX上运动,连接BQ,当ΔABC与ΔPQA全等时.BQ的长为()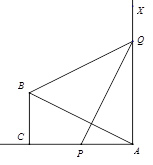
如图,矩形ABCD的面积为20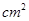 ,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B……依此类推,则平行四边形AOn-1CnB的面积为()
,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B……依此类推,则平行四边形AOn-1CnB的面积为()
A.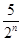 cm2 B.
cm2 B.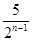 cm2
cm2
C.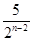 cm2 D.
cm2 D.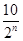 cm2
cm2
在平面直角坐标系中,抛物线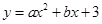 与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
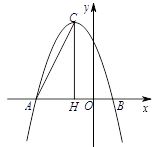

(1)a= ,b= ,顶点C的坐标为 .
(2)在 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
如图,平面直角坐标系xOy中,一次函数y=-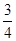 x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.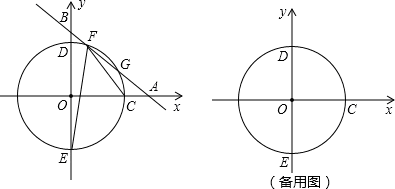
(1)若直线AB与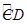 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.