如图，在平面直角坐标系xOy中，函数y=ax2+bx+1（a≠0）的图象与x的正半轴交于点A，与x的负半轴交于点B，与y轴交于点C．△PAC中，P（1，﹣1），∠P=90°，PA=PC．
（1）求点A的坐标．
（2）将△PAC沿AC翻折，若点P的对应点Q恰好落在函数y=ax2+bx+1（a≠0）的图象上，求a与b的值．
（3）将△ACO绕点A逆时针旋转90°得到△ADE，在x轴上取一点M，将∠PMD沿PM翻折，若点D的对应点F恰好落在x轴上，求点M的坐标．
如图，在方格纸上建立平面直角坐标系，线段AB的两个端点都在格点上，直线MN经过坐标原点，且点M的坐标是（1，2）。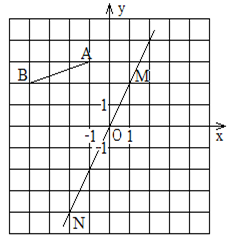
（1）写出点A、B的坐标；
（2）求直线MN所对应的函数关系式；
（3）作出线段AB关于直线MN的对称图形。
如图，已知□ABCD的对角线AC、BD相交于点O，AC =12，BD=18，且△AOB的周长l=23，求AB的长．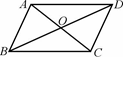
（1）计算: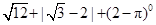
（2）解方程：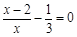
．
解方程(不等式组)
（1）
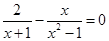
(2)
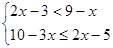
实践与探究：
对于任意正实数a、b，∵
≥0， ∴
≥0，∴
≥
只有当a＝b时，等号成立。
结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥
，只有当a＝b时，a+b有最小值。根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝时，
有最小值；
若m＞0，只有当m＝时，2
有最小值.
（2）如图，已知直线L1：
与x轴交于点A，过点A的另一直线L2与双曲线
相交于点B（2，m），求直线L2的解析式.
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1
于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.