(本小题满分12分).已知函数 .
.
(Ⅰ)求 的周期和振幅;
的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出 在一个周期内的图象.
在一个周期内的图象.
(Ⅲ)写出函数 的递增区间.
的递增区间.
(本小题满分12分) 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员,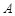 队队员是
队队员是 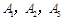 ,
,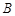 队队员是
队队员是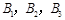 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
| 对阵队员 |
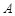 队队员胜的概率 队队员胜的概率 |
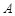 队队员负的概率 队队员负的概率 |
 对 对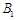 |
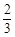 |
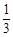 |
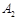 对 对 |
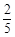 |
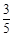 |
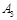 对 对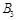 |
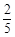 |
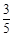 |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队,B队最后所得总分分别为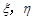 .
.
(1)求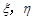 的概率分布列;
的概率分布列;
(2)求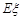 ,
,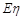 .
.
(本小题满分12分)已知函数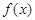 的定义域为
的定义域为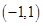 ,且同时满足下列条件:
,且同时满足下列条件:
(1)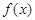 是奇函数;
是奇函数;
(2)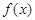 在定义域上单调递减;(3)
在定义域上单调递减;(3)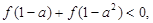 求
求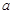 的取值范围.
的取值范围.
(本小题满分12分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过
检测,每一件二等品通过检测的概率为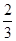 .现有10件产品,其中6件是一等品,4件是二等
.现有10件产品,其中6件是一等品,4件是二等
品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ) 随机选取3件产品,其中一等品的件数记为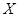 ,求
,求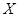 的分布列;
的分布列;
(Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.
(本小题满分12分)已知函数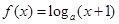 ,
,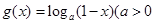 ,且
,且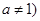
(1)求函数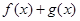 定义域
定义域
(2)判断函数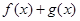 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(本小题12分)已知数列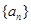 中,
中, ,且点
,且点 在直线
在直线 上.
上.
(1) 求数列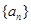 的通项公式;
的通项公式;
(2) 若函数 ,求证
,求证