如图,在四棱锥P一ABCD中,平面PAD⊥平面ABCD,AB∥DC,
△PAD是等边三角形,已知AD=4,BD= ,AB=2CD=8.
,AB=2CD=8.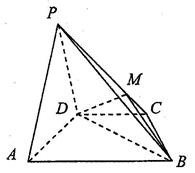
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?请证明你的结论;
(3)求四棱锥P—ABCD的体积.
如图,某公司要在
、
两地连线上的定点
处建造广告牌
,其中
为顶端,
长35米,
长80米,设
、
在同一水平面上,从
和
看
的仰角分别为
.
(1)设计中
是铅垂方向,若要求
,问
的长至多为多少(结果精确到0.01米)?
(2)施工完成后
与铅垂方向有偏差,现在实测得
,求
的长(结果精确到0.01米)?
设常数
,函数
.
(1)若
,求函数
的反函数
;
(2)根据
的不同取值,讨论函数
的奇偶性,并说明理由.
底面边长为2的正三棱锥
,其表面展开图是三角形
,如图,求
的各边长及此三棱锥的体积
.
设函数
,其中
是
的导函数.
,
(1)求
的表达式;
(2)若
恒成立,求实数
的取值范围;
(3)设
,比较
与
的大小,并加以证明.
如图,曲线
由上半椭圆
和部分抛物线
连接而成,
的公共点为
,其中
的离心率为
.
(1)求
的值;
(2)过点
的直线
与
分别交于
(均异于点
),若
,求直线
的方程.