(本小题满分12分)已知a、b、c分别是△ABC中角A、B、C的对边,且 .(Ⅰ)求角
.(Ⅰ)求角 的大小;(Ⅱ)若
的大小;(Ⅱ)若 ,求
,求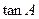 的值.
的值.
如图,P—ABCD是正四棱锥, 是正方体,其中
是正方体,其中
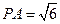
(1)求证: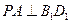 ;
;
(2)求平面PAD与平面 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(3)求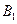 到平面PAD的距离
到平面PAD的距离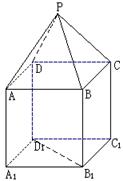
如图,在四棱锥 中,底面
中,底面 为正方形,且
为正方形,且 平面
平面 ,
, ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
(Ⅰ)证明:EF∥平面PCD;
(Ⅱ)求二面角B-CE-F的大小.
在正三棱锥 中,
中,
D是AC的中点, .
.
(1)求证:
(2)(理科)求二面角 的大小。
的大小。
(文科)求二面角 平面角的大小。
平面角的大小。
如图,已知点H在正方体 的对角线
的对角线 上,∠HDA=
上,∠HDA= .
.
(Ⅰ)求DH与 所成角的大小;
所成角的大小;
(Ⅱ)求DH与平面 所成角的大小.
所成角的大小.