去冬今春，某市部分地区遭受了罕见的旱灾，旱灾无情人有情．某单-优题课

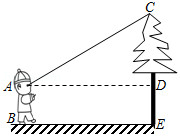
小丽用两锐角分别为 $30 °$ 和 $60 °$ 的三角尺测量一棵树的高度．如图，已知 $∠ CAD = 30 °$ ， $AB = DE = 1.75 m$ ， $BE = 6 m$ ，那么这棵树大约有多高？（结果精确到 $0.1 m$ ， $\sqrt{3} \approx 1.732)$

已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - (k + 1) = 0$ 有两个不相等的实数根，求 $k$ 的取值范围．

（1）计算： ${(π - 2019)}^{0} + | \sqrt{2} - 1 | + 2 \cos 45 °$ ；

（2）计算： $(1 + \frac{1}{x - 1}) \div \frac{x}{x^{2} - 1}$ ．

如图1，在平面直角坐标系 $xOy$ 中，抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴的负半轴交于点 $C$ ，已知抛物线的对称轴为直线 $x = \frac{\sqrt{3}}{2}$ ， $B$ 、 $C$ 两点的坐标分别为 $B (2 \sqrt{3}$ ， $0)$ ， $C (0, - 3)$ ．点 $P$ 为直线 $BC$ 下方的抛物线上的一个动点（不与 $B$ 、 $C$ 两点重合）．

（1）求此抛物线的解析式；

（2）如图1，连接 $PB$ 、 $PC$ 得到 $ΔPBC$ ，问是否存在着这样的点 $P$ ，使得 $ΔPBC$ 的面积最大？如果存在，求出面积的最大值和此时点 $P$ 的坐标；如果不存在，请说明理由．

（3）如图2，连接 $AP$ 交线段 $BC$ 于点 $D$ ，点 $E$ 为线段 $AD$ 的中点，过点 $D$ 作 $DM ⊥ AB$ 于点 $M$ ， $DN ⊥ AC$ 于点 $N$ ，连接 $EM$ 、 $EN$ ，则在点 $P$ 的运动过程中， $∠ MEN$ 的大小是否为定值？如果是，求出这个定值；如果不是，请说明理由．

如图， $AB$ 是 $⊙ O$ 的直径，点 $C$ 为 $⊙ O$ 上一点， $OE ⊥ BC$ 于点 $H$ ，交 $⊙ O$ 于点 $E$ ，点 $D$ 为 $OE$ 的延长线上一点， $DC$ 的延长线与 $BA$ 的延长线交于点 $F$ ，且 $∠ BOD = ∠ BCD$ ，连结 $BD$ 、 $AC$ 、 $CE$ ．

（1）求证： $DF$ 为 $⊙ O$ 的切线；

（2）过 $E$ 作 $EG ⊥ FD$ 于点 $G$ ，求证： $ΔCHE ≅ ΔCGE$ ；

（3）如果 $AF = 1$ ， $\sin ∠ FCA = \frac{\sqrt{3}}{3}$ ，求 $EG$ 的长．