下列语句:
①每一个外角都等于60°的多边形是六边形;
②“反证法”就是举反例说明一个命题是假命题;
③“等腰三角形两底角相等”的逆命题是真命题;
④分式有意义的条件是分子为零且分母不为零.
其中正确的个数为( )
| A.1 | B.2 | C.3 | D.4 |
如图,在四边形ABCD中,E,F分别为DC、AB的中点,G是AC的中点,则EF与AD+CB的关系是()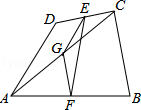
A.2EF=AD+BC B.2EF>AD+BC C.2EF<AD+BC D.不确定
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是()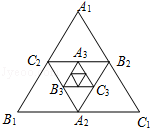
A.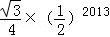 |
B.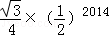 |
C.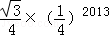 |
D.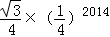 |
如图,△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD:S△ABC=()
| A.1:2 | B.1:4 | C.1:3 | D.2:3 |
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则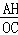 的值为()
的值为()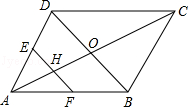
| A.1 | B.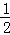 |
C.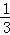 |
D.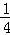 |
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90°+ ∠A;
∠A;
②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;
③EF是△ABC的中位线;
④设OD=m,AE+AF=n,则S△AEF= mn.
mn.
其中正确的结论是()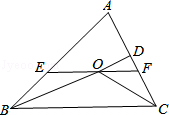
A.①②③ B.①③④ C.②③④ D.①②④