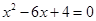如图,抛物线y=ax2+bx﹣ 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.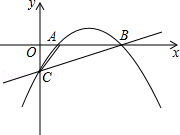
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.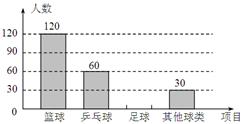
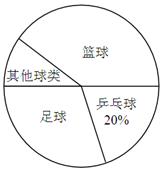
请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有人,在扇形图中,表示“其他球类”的扇形的圆心角为度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有人.
某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到元购物券,至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
在数学课上,陈老师在黑板上画出如图所示的图形,在△AEC和△DFB中,已知∠E=∠F,点A,B,C,D在同一直线上,并写下三个关系式:①AE∥DF,②AB=CD,③CE=BF.请同学们从中再任意选取两个作为补充条件,剩下的那个关系式作为结论构造命题.小明选取了关系式①,②作为条件,关系式③作为结论.你认为按照小明的选法得到的命题是真命题吗?如果是,请写出证明过程,如果不是,请举出反例.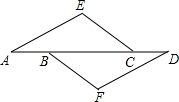
解不等式组: .
.
解方程: