已知抛物线
经过A（﹣1，0），B（3，0）两点，与y轴相交于点C，该抛物线的顶点为点D．
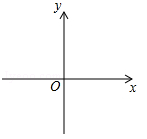
（1）求该抛物线的解析式及点D的坐标；
（2）连接AC，CD，BD，BC，设△AOC，△BOC，△BCD的面积分别为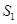
，
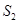和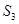
，用等式表示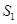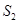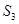，、之间的数量关系，并说明理由；
（3）点M是线段AB上一动点（不包括点A和点B），过点M作MN∥BC交AC于点N，连接MC，是否存在点M使∠AMN=∠ACM？若存在，求出点M的坐标和此时刻直线MN的解析式；若不存在，请说明理由．
每题6分）如图，EF⊥GF于F．∠AEF=150°，∠DGF=60°，试判断AB和CD的位置关系，并说明理由
解下列方程组（5分
2）
（1）
（2）
已知AD∥BC，AB∥CD，E为射线BC上一点，AE平分∠BAD．
（1）如图1，当点E在线段BC上时，求证：∠BAE=∠BEA．
（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE=3∠CDE，∠AED=60°．
①求证∠ABC=∠ADC；
②求∠CED的度数．
“龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．
（1）填空：折线OABC表示赛跑过程中的路程与时间的关系，线段OD表示赛跑过程中的路程与时间的关系．赛跑的全程是 米．
（2）兔子在起初每分钟跑米，乌龟每分钟爬米．
（3）乌龟用了分钟追上了正在睡觉的兔子．
（4）兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了0．5分钟，请你算算兔子中间停下睡觉用了多少分钟？
如图，已知∠ABC=63°，∠ECB=117°，∠P=∠Q．
（1）AB与ED平行吗？为什么？
（2）∠1与∠2是否相等？说说你的理由．