为了解全校学生上学的交通方式,该校九年级(8)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题: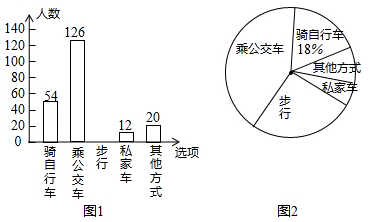
(1)本次接受调查的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.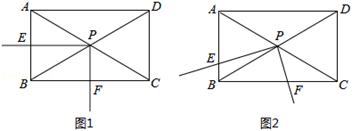
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为;
的值为;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.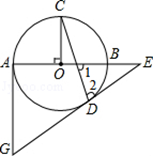
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.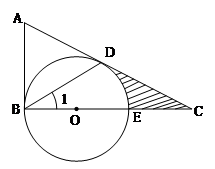
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均的每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为万元.
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕着点B逆时针旋转90°,得到△A1BC1,请画出△A1BC1;求点A旋转过程中所经过的路径长。
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.