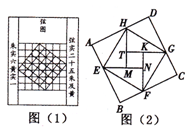
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)),图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为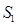 、
、 、
、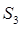 .若正方形EFGH的边长为2,则
.若正方形EFGH的边长为2,则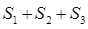 = .
= .
(本题6分)已知:如图,射线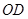 、
、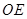 分别是
分别是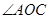 、
、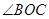 的角平分线,如果
的角平分线,如果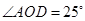 ,
,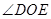 比
比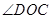 的
的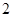 倍还多
倍还多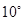 ,求
,求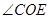 和
和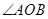 的度数.
的度数.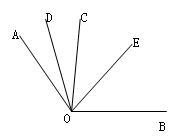
(本题6分)下图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图.
如图,直角坐标系中,点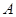 的坐标为
的坐标为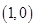 ,以线段
,以线段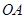 为边在第四象限内作等边
为边在第四象限内作等边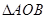 ,点
,点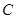 为
为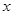 正半轴上一动点
正半轴上一动点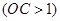 ,连结
,连结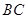 ,以线段
,以线段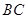 为边在第四象限内作等边
为边在第四象限内作等边 ,直线
,直线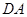 交
交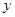 轴于点
轴于点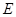 .
.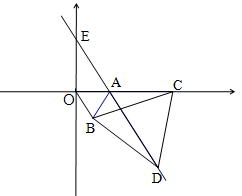
(1)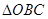 与
与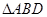 全等吗?判断并证明你的结论;
全等吗?判断并证明你的结论;
(2)将等边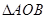 沿
沿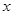 轴翻折,
轴翻折,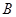 点的对称点为
点的对称点为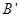 .
.
①点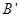 会落在直线
会落在直线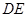 上么?请说明理由;
上么?请说明理由;
②随着点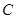 位置的变化,点
位置的变化,点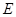 的位置是否会发生变化? 若没有变化,请直接写出点
的位置是否会发生变化? 若没有变化,请直接写出点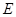 ,若有变化,请说明理由.
,若有变化,请说明理由.
已知某种水果的批发单价与批发量的函数关系如图所示.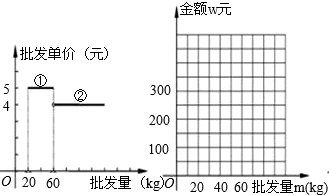
(1)请说明图中①、②两段函数图象的实际意义.
(2)写出批发该种水果的资金金额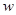 (元)与批发量
(元)与批发量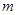 (
(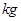 )之间的函数关系式;在图中的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
)之间的函数关系式;在图中的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
某地举办乒乓球比赛的费用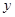 (元)包括两部分:一部分是租用比赛场地等固定不变的费用
(元)包括两部分:一部分是租用比赛场地等固定不变的费用 ,另一部分与参加比赛的人数
,另一部分与参加比赛的人数 (人)成正比例. 当
(人)成正比例. 当 时,
时,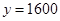 ,当
,当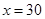 时,
时,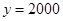 .
.
(1)求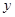 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果有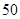 名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?
名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?