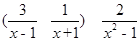如图,在平行四边形
中,
.

(1)利用尺规作图,在
边上确定点
,使点
到边
,
的距离相等(不写作法,保留作图痕迹);
(2)若
则
=.
有A、B两只不透明的布袋,A袋中有四个除标号外其他完全相同的小球,标号分别为0、1、2、3;B袋中有三个除标号外其他完全相同的小球,标号分别为-2、-1、0。小明先从A袋中随机取出一小球,用m表示该球的标号,再从B袋中随机取出一球,用n表示该球的标号。
(1)用树状图或列表的方式表示(m、n)的所有可能结果。
(2)若m、n分别表示数轴上两个点,求这两个点之间的距离不大于3的概率。
根据某研究中心公布的近几年中国互联网络发展状况统计报告的部分相关数据,绘制的统计图表如下:
根据以上信息解答下列问题:
(1)直接写出扇形统计图中m的值为;
(2)从2011年到2014年,中国网民人数每年增长的人数近似相等,估算2015年中国网民的人数约为亿;
(3)据我市统计数据显示,2014年末全市常住人口为650万人,其中网民数约为420万人.若2014年我市的网民学历结构与2014年的中国网民学历结构基本相同,请你估算2014年末我市网民中学历是大专和大学本科及以上的约有多少万人?
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出 的值为(不必写出计算过程).
的值为(不必写出计算过程).
(1) 解方程: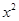 ﹣4x-5=0;
﹣4x-5=0;
(2) 解不等式组
(1)计算: +2sin30°-
+2sin30°-
(2)计算: