如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．
（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）
如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F.
(1)求证：AC是⊙O的切线；
(2)已知sin A＝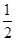
，⊙O的半径为4，求图中阴影部分的面积．
如下图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置，设BC＝1，AC＝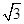
，则顶点A运动到点A″的位置时．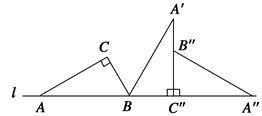
求：(1)点A经过的路线的长度；
(2)点A经过的路线与直线l所围成的面积(计算结果保留π)．
如图AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C作DC⊥OA，交AB于点D.
(1)求证：∠CDO＝∠BDO；
(2)若∠A＝30°，⊙O的半径为4，求阴影部分的面积(结果保留π)．
如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E.
(1)求证：直线BD与⊙O相切；
(2)若AD：AE＝4：5，BC＝6，求⊙O的直径．
如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF于点H，交⊙O于点C，连接BD.
(1)求证：BD平分∠ABH；
(2)如果AB＝12，BC＝8，求圆心O到BC的距离．