解方程: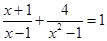 .
.
为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有 , 两种型号的健身器材可供选择.
(1)劲松公司2015年每套 型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套 型健身器材年平均下降率 ;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司 , 两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套 型健身器材售价为1.6万元,每套 型健身器材售价为 万元.
① 型健身器材最多可购买多少套?
②安装完成后,若每套 型和 型健身器材一年的养护费分别是购买价的 和 ,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
已知关于 的一元二次方程 有两个实数根 , .
(1)求 的取值范围;
(2)若 , 满足 ,求 的值.
计算: .
如图,矩形 的两边在坐标轴上,点 的坐标为 ,抛物线 过点 , 两点,且与 轴的一个交点为 ,点 是线段 上的动点,设 .
(1)请直接写出 、 两点的坐标及抛物线的解析式;
(2)过点 作 ,交抛物线于点 ,连接 ,当 为何值时, ?
(3)点 是 轴上的动点,过点 作 ,交 于点 ,作 ,交 于点 ,当四边形 为正方形时,请求出 的值.

如图,在 中, , 是中线, ,一个以点 为顶点的 角绕点 旋转,使角的两边分别与 、 的延长线相交,交点分别为点 , , 与 交于点 , 与 交于点 .
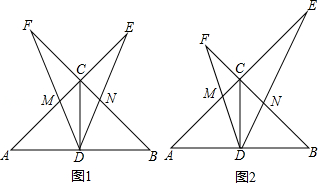
(1)如图1,若 ,求证: ;
(2)如图2,在 绕点 旋转的过程中:
①探究三条线段 , , 之间的数量关系,并说明理由;
②若 , ,求 的长.