甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
(1)请填写下表:
| |
平均数 |
方差 |
中位数 |
空气质量为优的次数 |
| 甲 |
80 |
|
|
|
| 乙 |
80 |
1060 |
|
|
(2)请回答下面问题
①从平均数和中位数来分析,甲,乙两城市的空气质量.
②从平均数和方差来分析,甲,乙两城市的空气质量情况.
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.
计算: .
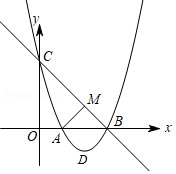
已知抛物线 过点 , 两点,与 轴交于点 , .
(1)求抛物线的解析式及顶点 的坐标;
(2)过点 作 ,垂足为 ,求证:四边形 为正方形;
(3)点 为抛物线在直线 下方图形上的一动点,当 面积最大时,求点 的坐标;
(4)若点 为线段 上的一动点,问: 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“ :文明礼仪, :生态环境, :交通安全, :卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.

(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“ ”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
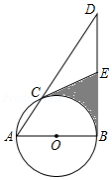
如图, 为 的直径,且 ,点 是 上的一动点(不与 , 重合),过点 作 的切线交 的延长线于点 ,点 是 的中点,连接 .
(1)求证: 是 的切线;
(2)当 时,求阴影部分面积.
天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道 处开始,沿 路线对索道进行检修维护.如图:已知 米, 米, 与水平线 的夹角是 , 与水平线 的夹角是 .求:本次检修中,检修人员上升的垂直高度 是多少米?(结果精确到1米,参考数据:
