小明妈妈,每天需赶头班公交车,驶往终点站.离他家最近的公交站点离终点站15km,一天他妈妈从家步行到公交站点,恰好赶上头班公交车,上车后才发现有重要物品落在家中,急忙通知小明将物品送到终点站,这时妈妈已上车5min,小明马上取了东西,用时6min赶到妈妈上车的公交站点,乘坐刚好路过的出租车,沿公交车的线路驶往公交车的终点站,结果比公交车早4min到达,出租车与小明一起等候公交车.若公交车,出租车均视为全程匀速行驶,出租车的速度为60km/h(即:1km/min).设妈妈所乘公交车离开她上车的站点的时间为t(min),小明上车后,小明所乘出租车距妈妈上车的公交站点的路程为S1(km),妈妈所乘的公交车与小明所乘出租车之间相距的路程为S(km)
(1)求S1与t之间的函数关系式,并写出t的取值范围;
(2)写出11≤t≤30,S与t之间的函数关系式;
(3)公交车到达终点之前,经多长时间两车相距500m.
你能找出规律吗?
(1)计算: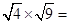 ,
, 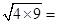 .
.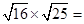 ,
, 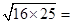 .
.
(2)请按找到的规律计算:①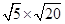 ;②
;②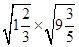
(3)已知: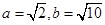 ,则
,则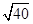 =(用含
=(用含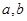 的式子表示)。
的式子表示)。
先化简,再求值: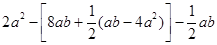 ,其中
,其中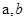 满足
满足
请将下列实数在数轴上表示出来,并把这些数按从小到大的顺序排列,用“<”连接。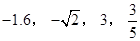
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=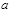 ,其中
,其中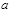 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并给出证明.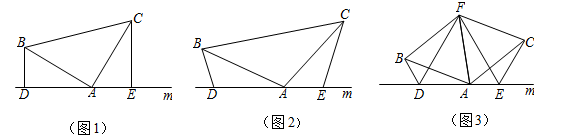
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,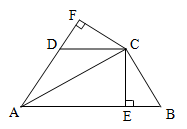
(1)证明:Rt△BCE≌Rt△DCF;
(2)若AB=21,AD=9, BC=CD=10,求AC的长.