已知 ,
, 为圆
为圆 :
: 与
与 轴的交点(A在B上),过点
轴的交点(A在B上),过点 的直线
的直线 交圆
交圆 于
于 两点.
两点.
(1)若弦 的长等于
的长等于 ,求直线
,求直线 的方程;
的方程;
(2)若 都不与
都不与 ,
, 重合时,是否存在定直线
重合时,是否存在定直线 ,使得直线
,使得直线 与
与 的交点恒在直线
的交点恒在直线 上.若存在,求出直线
上.若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分)
设等差数列 的前
的前 项和为
项和为 ,等比数列
,等比数列 的前
的前 项和为
项和为 ,已知
,已知
 .
.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)求和: .
.
(本小题满分12分)
如图,在三棱锥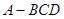 中,面
中,面 面
面 ,
,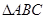 是正三角形,
是正三角形,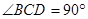 .
.
(Ⅰ)求证: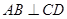 ;
;
(Ⅱ)若异面直线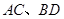 所成角的余弦值为
所成角的余弦值为 ,求二面角
,求二面角 的大小;
的大小;
(本小题满分12分)
质地均匀的正四面体玩具的4个面上分别刻着数字1,2,3,4。将4个这样的玩具同时抛掷于桌面上。
(Ⅰ)设 为与桌面接触的4个面上数字中偶数的个数,求
为与桌面接触的4个面上数字中偶数的个数,求 的分布列及期望E
的分布列及期望E ;
;
(Ⅱ)求与桌面接触的4个面上的4个数的乘积能被4整除的概率。
(本小题满分10分)
在⊿ 中,角
中,角 的对边分别为
的对边分别为 ,且
,且
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分12分)
已知公差不为零的等差数列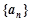 的前4项和为10,且
的前4项和为10,且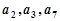 成等比数列.
成等比数列.
(Ⅰ)求通项公式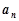 ;
;
(Ⅱ)设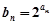 ,求数列
,求数列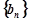 的前
的前 项和
项和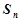 .
.