一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
有4个不同的球,4个不同的盒子,现在要把球全部放入盒内.
(1)共有几种放法?
(2)恰有一个盒不放球,共有几种放法?
若(2+x+x2) 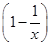 3的展开式中的常数项为a,求
3的展开式中的常数项为a,求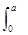 (3x2-1)dx.
(3x2-1)dx.
四张卡片上分别标有数字“2”“0”“0”“9”,其中“9”可当“6”用,则由这四张卡片可组成不同的四位数有多少个?
如图,点P(0,-1)是椭圆C1: =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.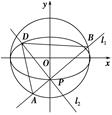
(1)求椭圆C1的方程;
(2)求当△ABD的面积取最大值时,直线l1的方程.