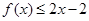已知二次函数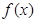 满足条件
满足条件 ,及
,及 .
.
(1)求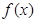 的解析式;
的解析式;
(2)求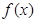 在
在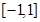 上的最值.
上的最值.
已知曲线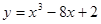
(1)求曲线在点 处的的切线方程;
处的的切线方程;
(2)过原点作曲线的切线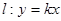 ,求切线方程.
,求切线方程.
已知函数 且
且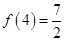 ,
,
(1)求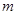 的值;
的值;
(2)判断 在
在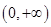 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.
已知函数f(x)=x3+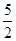 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+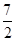 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为 ,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
设函数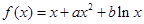 ,曲线
,曲线 过P(1,0),且在P 点处的切线斜率为2.
过P(1,0),且在P 点处的切线斜率为2.
(1)求a,b的值;
(2)证明: