在 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且
(1)求 的大小;
的大小;
(2)若 ,试求内角B、C的大小.
,试求内角B、C的大小.
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
(1)求x,y ;
(2)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。
如右下图,在长方体ABCD—A1B1C1D1中,已知AB=" 4," AD ="3," AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C—DE—C1的余弦值;
(2) 求直线EC1与FD1所成的余弦值.
在 中,
中, 分别是角
分别是角 的对边,
的对边, 且
且
(1)求 的面积;
的面积;
(2)若 ,求角
,求角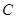 。
。
如图,在棱长为a的正方体ABCD—A1B1C1D1中,M为A1D中点,N为AC中点.
(1)求异面直线MN和AB所成的角;
(2)求证:MN⊥AB1;