(本小题满分12分) ;(2)
;(2)
对于5年可成材的树木,从栽种到5年成材的木材年生长率为18%,以后木材的年生长率为10%.树木成材后,既可以出售树木,重栽新树苗;也可以让其继续生长.问:哪一种方案可获得较大的木材量?(注:只需考虑10年的情形)(参考数据:lg2=0.3010,lg1.1=0.0414)
已知集合A={m|正整数指数函数y=(m2+m+1)•( )x,x∈N+},求集合A.
)x,x∈N+},求集合A.
已知正整数指数函数f(x)的图象经过点(3,27),
(1)求函数f(x)的解析式;
(2)求f(5);
(3)函数f(x)有最值吗?若有,试求出;若无,说明原因.
如图(1)是一辆汽车速度随时间而变化的情况示意图.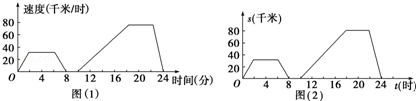
(1)汽车从出发到最后停止共经过多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)如果纵轴表示路程s(千米).如图(2),横轴表示时间t(时).这是一个骑自行车者离家距离与时间的关系图象.在出发后8小时到10小时之间可能发生了什么情况?骑自行车者在哪些时间段保持匀速运动?速度分别是多少?
在日常生活中,我们常常会用到弹簧秤,下表为用弹簧秤称物品时弹簧秤的伸长长度与物品质量之间的关系:
| 弹簧秤的伸长长度(cm) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
| 物品质量(kg) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
如果用y表示弹簧秤的伸长长度,x表示物品质量,则
(1)随x的增大,y的变化趋势是怎样的?
(2)当x=3.5时,y等于多少?当x=8时呢?
(3)写出x与y之间的关系式.