(本小题满分12分)对于给定数列{an},如果存在实常数p,q,使得an+1=pan+q对于任意n∈N*都成立,我们称数列{an}是“M类数列”.
(1)已知数列{bn}是“M类数列”且bn= 3n 求它对应的实常数p,q的值;
(2)若数列{cn}满足c1=-l,cn - cn+l =2n(n∈N*),求数列{cn}的通项公式.判断{cn}是否为“M类数列”并说明理由。
袋中装有编号为 的球
的球 个,编号为
个,编号为 的球
的球 个,这些球的大小完全一样。
个,这些球的大小完全一样。
(1)从中任意取出四个,求剩下的四个球都是 号球的概率;
号球的概率;
(2)从中任意取出三个,记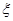 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量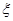 的分布列及其数学期望
的分布列及其数学期望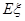 .
.
已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.
设 为三角形
为三角形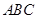 的三边,求证:
的三边,求证: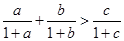
已知圆 的方程为
的方程为 ,直线
,直线
 ,设点
,设点 .
.
(1)若点 在圆
在圆 外,试判断直线
外,试判断直线 与圆
与圆 的位置关系;
的位置关系;
(2)若点 在圆
在圆 上,且
上,且 ,
, ,过点
,过点 作直线
作直线 分别交圆
分别交圆 于
于 两点,且直线
两点,且直线 和
和 的斜率互为相反数;
的斜率互为相反数;
① 若直线 过点
过点 ,求
,求 的值;
的值;
② 试问:不论直线 的斜率怎样变化,直线
的斜率怎样变化,直线 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.
设 是数列
是数列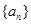 的前
的前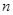 项和,且
项和,且 .
.
(1)当 ,
, 时,求
时,求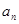 ;
;
(2)若数列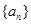 为等差数列,且
为等差数列,且 ,
,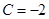 .
.
①求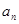 ;
;
②设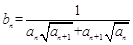 ,且数列
,且数列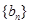 的前
的前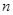 项和为
项和为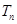 ,求
,求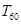 的值.
的值.