已知两直线 和
和 ,试确定
,试确定 ,
, 的值,使(1)
的值,使(1) ;(2)
;(2) ,且
,且 在
在 轴上的截距为-1.
轴上的截距为-1.
一个长方体的各顶点均在同一个球的球面上,且一个顶点上的三条棱的长分别为1,2,3,求此球的表面积与体积
(文)以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y=17时的概率。
(注:方差 ,其中
,其中 为
为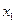 ,
, ,……
,……  的
的
平均数)
(理)某种产品的质量以其质量指标值衡量,质量指标越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每产品的质量指标值,得到时下面试验结果:
A配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110] |
| 频数 |
8 |
20 |
42 |
22 |
8 |
B配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110] |
| 频数 |
4 |
12 |
42 |
32 |
10 |
(I)分别估计用A配方,B配方生产的产品的优质品率;
(II)已知用B配方生产的一种产品利润y(单位:元)与其质量指标值t的关系式为
从用B配方生产的产品中任取一件,其利润记为X(单位:元).求X的分布列及数学期
望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概
率).
(文)每次抛掷一枚骰子(六个面上分别标以数字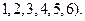
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
(理)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中所有的白球的个数;
(II)求随机变量 的概率分布;
的概率分布;
(III)求甲取到白球的概率.