已知函数 ,其中
,其中
(1)判别函数 的奇偶性;
的奇偶性;
(2)判断并证明函数 在
在 上单调性;
上单调性;
(3)是否存在这样的负实数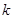 ,使
,使 对一切
对一切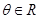 恒成立,若存在,试求出k取值的集合;若不存在,说明理由.
恒成立,若存在,试求出k取值的集合;若不存在,说明理由.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量 (毫克)与时间
(毫克)与时间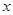 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数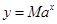 (
( 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数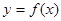 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?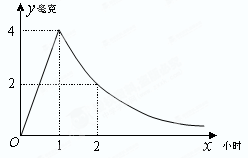
计算下列各式的值:
(1)设 ,求
,求 的值;
的值;
|
(2)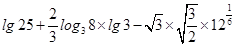 .
.
已知全集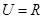 ,函数
,函数 的定义域为集合
的定义域为集合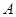 ,集合
,集合 =
= <
< <
<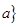 .
.
(1)求集合 ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分16分)
已知函数 是偶函数.
是偶函数.
(1)求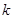 的值;
的值;
(2)设函数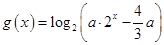 ,其中
,其中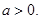 若函数
若函数 与
与 的图象有且只有一个交点,求
的图象有且只有一个交点,求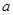 的取值范围.
的取值范围.
已知函数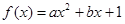 (
( ∈R且
∈R且 ),
),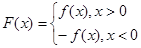 .
.
(Ⅰ)若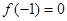 ,且函数
,且函数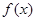 的值域为[0, +
的值域为[0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时,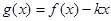 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设 ,
,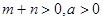 , 且
, 且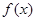 是偶函数,判断
是偶函数,判断 是否大于零?
是否大于零?