已知函数 是定义在
是定义在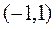 上的奇函数,且
上的奇函数,且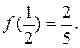
(1)确定函数 的解析式;
的解析式;
(2)判断并证明 在
在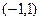 的单调性;
的单调性;
(3)解不等式
设命题 :函数
:函数 =x3-ax-1在区间
=x3-ax-1在区间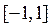 上单调递减;命题
上单调递减;命题 :函数
:函数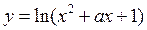 的值域是
的值域是 .如果命题
.如果命题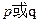 为真命题,
为真命题,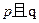 为假命题,求
为假命题,求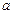 的取值范围.
的取值范围.
已知函数 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x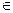 (-∞,-3)
(-∞,-3)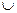 (2,+∞)时,
(2,+∞)时,  <0,当x
<0,当x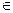 (-3,2)时
(-3,2)时 >0 .
>0 .
(1)求 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
已知函数  (a>0)
(a>0)
(1)判断并证明y= 在x∈(0,+∞)上的单调性;
在x∈(0,+∞)上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求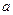 的值,并求出不动点
的值,并求出不动点 ;
;
(3)设 =
= ,若y=
,若y= 在(0,+∞)上有三个零点 , 求
在(0,+∞)上有三个零点 , 求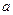 的取值范围.
的取值范围.
已知数列 的前n项和为
的前n项和为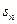 ,
,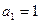 且满足
且满足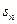 =2
=2 +n (n>1且n
+n (n>1且n ∈
∈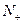 )
)
(1)求数列 的通项公式和前n项的和
的通项公式和前n项的和
(2)设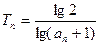 ,求使得不等式
,求使得不等式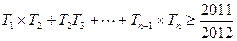 成立的最小正整数n的值
成立的最小正整数n的值