直线l经过点(3,2),且在两坐标轴上的截距相等,求直线l的方程.
求斜率为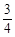 ,且与两坐标轴所围成的三角形的周长是12的直线方程.
,且与两坐标轴所围成的三角形的周长是12的直线方程.
圆柱内有一个直四棱柱,直四棱柱底面是圆柱底面的内接正方形.已知圆柱表面积为6 ,且底面圆直径与母线长相等,求此四棱柱的体积.
,且底面圆直径与母线长相等,求此四棱柱的体积.
已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的零点;
的零点;
(Ⅱ)若关于 的方程
的方程 在
在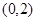 上有2个不同的解
上有2个不同的解 ,求
,求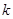 的取值范围,并证明:
的取值范围,并证明: .
.
季节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
(Ⅰ)试建立价格P与周次t之间的函数关系式;
(Ⅱ)若此服装每件进价Q与周次t之间的关系为 ,
, ,
, ,试问该服装第几周每件销售利润最大,最大值是多少?
,试问该服装第几周每件销售利润最大,最大值是多少?
(注:每件销售利润=售价-进价)
(本小题满分12分)
设 是定义在
是定义在 上的函数,满足条件:
上的函数,满足条件:
① ; ②当
; ②当 时,
时, 恒成立.
恒成立.
(Ⅰ)判断 在
在 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若 ,求满足
,求满足 的x的取值范围.
的x的取值范围.