(本小题满分16分)在数列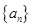 中,
中,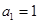 ,
,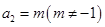 ,前
,前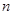 项和
项和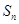 满足
满足 .
.
(1)求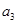 (用
(用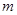 表示);
表示);
(2)求证:数列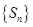 是等比数列;
是等比数列;
(3)若 ,现按如下方法构造项数为
,现按如下方法构造项数为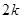 的有穷数列
的有穷数列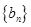 :当
:当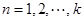 时,
时,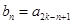 ;当
;当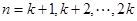 时,
时,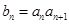 ,记数列
,记数列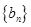 的前
的前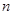 项和
项和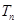 ,试问:
,试问: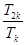 是否能取整数?若能,请求出
是否能取整数?若能,请求出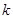 的取值集合;若不能,请说明理由.
的取值集合;若不能,请说明理由.
.设函数 且
且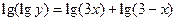 。
。
(Ⅰ)求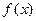 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求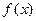 的值域。
的值域。
已知函数 .
.
(Ⅰ)当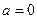 时,求曲线
时,求曲线 在
在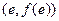 处的切线方程(
处的切线方程(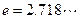 )
)
(Ⅱ)已知 为函数
为函数 的极值点,求函数
的极值点,求函数 的单调区间。
的单调区间。
(本小题满分10分)选修4-5:不等式选讲
已知函数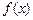 =|x-2|
=|x-2|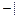 x-5|.
x-5|.
(I)证明: ≤
≤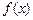 ≤3;
≤3;
(II)求不等式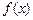 ≥x2
≥x2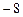 x+15的解集.
x+15的解集.
(本小题满分10分)选修4-4:坐标系统与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为 (
( 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为 (
(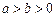 ,
, 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ= 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当 =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当 =
=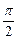 时,这两个交点重合.
时,这两个交点重合.
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当 =
=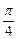 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 =
=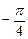 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
(本小题满分10分)选修4-1:几何证明选讲
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(I)证明:CD//AB;
(II)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.