(1)利用“五点法”画出函数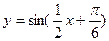 在长度为一个周期的闭
在长度为一个周期的闭
区间的简图
列表: 作图:
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样的变换得到。
R)的图象经过怎样的变换得到。
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为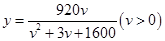 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
已知曲线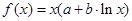 过点P(1,3),且在点P处的切线
过点P(1,3),且在点P处的切线
恰好与直线 垂直.求 (Ⅰ) 常数
垂直.求 (Ⅰ) 常数 的值; (Ⅱ)
的值; (Ⅱ)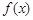 的单调区间.
的单调区间.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.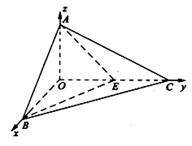
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.
已知p: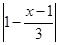 ≤2; q:
≤2; q: ≤0(m>0),若
≤0(m>0),若 是
是 的充分而不必要条件,求实数m的取值范围.
的充分而不必要条件,求实数m的取值范围.
在 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是 、b、c,已知
、b、c,已知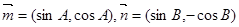 ,且
,且 的夹角为
的夹角为 。
。
(Ⅰ)求内角C的大小;
(Ⅱ)已知 ,三角形的面积
,三角形的面积 ,求
,求 的值。
的值。