如图,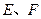 是平行四边形
是平行四边形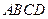 的对角线
的对角线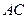 上的点,
上的点,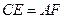 ,请你猜想:线段
,请你猜想:线段 与线段
与线段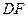 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。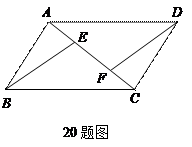
我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了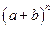 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应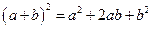 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着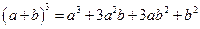 展开式中的系数等等。
展开式中的系数等等。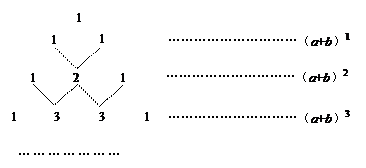
(1)根据上面的规律,写出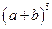 的展开式。
的展开式。
(2)利用上面的规律计算: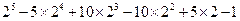
计算: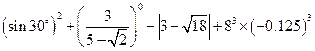
在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数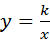 (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F.
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.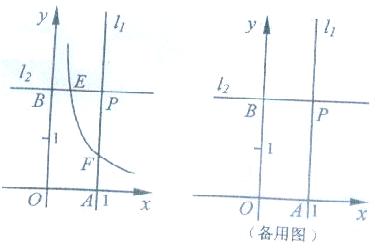
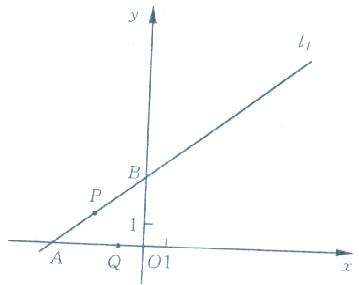
在平面直角坐标系XOY中,一次函数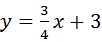 的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值.