在平面直角坐标系XOY中,一次函数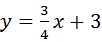 的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1,l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值.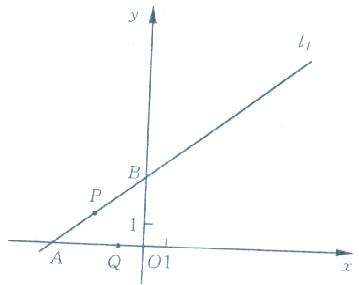
从2开始,连续的偶数相加,它们和的情况如下表:
| 加数的个数n |
S |
| 1 |
2=1×2 |
| 2 |
2+4=6=2×3 |
| 3 |
2+4+6=12=3×4 |
| 4 |
2+4+6+8=20=4×5 |
| 5 |
2+4+6+8+10=30=5×6 |
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100 的值.
的值.
出租车司机小石某天下午营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-3,+14,-11,+10,-12.
(1)将最后一名乘客送达目的地时,小石距下午出发地点的距离是多少千米?
(2)若汽车耗油量为0.3升/千米,这天下午汽车耗油共多少升?
已知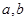 互为倒数,
互为倒数,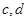 互为相反数,
互为相反数,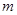 的绝对值为2,求
的绝对值为2,求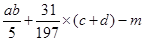 的值
的值
(1)若我们把不小于x的最小整数记作〈x〉,如〈2.4〉=3,〈-1.5〉=-1;则〈3〉= ,〈-2.2〉=
(2)在我国,出租车已经普及,杭州城区A、B两种出租车,它们的收费方式有所不同, A种出租车的收费方式是:每千米收费2.5元,不收其它费用。B种出租车的收费方式是:行程不超过3千米收费8元,超过3千米后超出部分每千米再增收2元,同时每趟营运在计价器显示的金额外再向乘客加收1元的燃料附加费.(注:两种出租车在路程上不足1千米按1千米计算,如6.1千米应算成7千米)若某公司员工小王需要乘出租车到离家x千米的公司上班。
①请利用题(1)中的符号,用代数式表示小王分别使用A、B两种出租车的收费情况。
②分别求出x=4.5;x=6;x=6.1时A、B两种出租车的收费情况.
③结合②的答案请说一说小王为了省钱应该如何选择出租车。
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有 张桌子时,两种摆放方式各能坐多少人?
张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?